FDCL home

 

Current research projects:

UCI Rocket Project

Past Projects

People

K.D. Mease

Contact

 

For any technical issue, contact the webmaster.

Web last revised:
October 24, 2010

 

University of California, Irvine

Methodology for Nonlinear Multiple Time Scale Dynamical Systems

Sponsored by the National Science Foundation
Research begun in collaboration with S.H. Lam, Princeton University


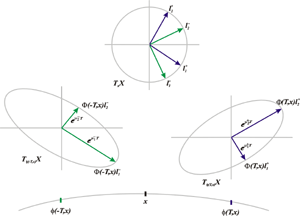
Nonlinear Time Scales

The project objective is to develop a methodology for the analysis and design of nonlinear dynamical systems that have an underlying multiple time-scale structure. The presence of two or more widely separated time-scales offers the opportunity for reduced-order analysis and design, yet at the present time there is no general methodology for uncovering and exploiting time-scale separation in nonlinear systems. We are developing a general methodology for time-scale identification and reduced-order model development for high-order nonlinear systems - systems that arise in the context of analyzing and designing machines, processes, structures, ground and aerospace vehicles, robots, and other mechanical systems.

 

References:

K.D. Mease, U. Topcu, and E. Aykutlug, Characterizing Two-Timescale Nonlinear Dynamics Using Finite-Time Lyapunov Exponents and Vectors, arXiv:0807.0239 [math.DS], 2008.

E.Aykutlug and K. D. Mease, Approximate Solution of Hypersensitive Optimal Control Problems Using Finite-Time Lyapunov Analysis, American Control Conference, St. Louis, Missouri, June 2009.

Mease, K.D. and Topcu, U., “Two-Timescale Nonlinear Dynamics and Slow Manifold Determination”, AIAA GNC-Conference, San Francisco, Aug. 2005

Mease, K.D., “Multiple Time-Scales in Nonlinear Flight Mechanics: Diagnosis and Modeling", Applied Mathematics and Computation, Vol. 164, No. 2, pp. 627—648, 2005

K. D. Mease, S. Bharadwaj, and S. Iravanchy, "Timescale Analysis for Nonlinear Dynamical Systems", J. of Guidance, Control, and Dynamics, Vol. 26, No. 2, March–April 2003, pp. 318-330

K. D. Mease, S. Iravanchy, S. Bharadwaj, M. Fedi, "Time Scale Analysis for Nonlinear Systems," Paper 2000-4591, AIAA GNC-Conference, Denver, Aug. 2000

A. V. Rao, "Application of a Dichotomic Basis Method to Performance Optimization of Supersonic Aircraft," J. of Guidance, Control, and Dynamics, Vol. 23, No. 3, pp. 570-573, 2000

A. V. Rao and K. D. Mease, "Eigenvector Approximate Dichotomy Basis Method for Solving Hyper-Sensitive Optimal Control Problems," Optimal Control: Applications and Methods, Vol. 21, pp. 1-19, 2000

S. Bharadwaj and K. D. Mease, "Geometric Structure of Multiple Time-Scale Nonlinear Systems," Proceedings of the 14th World Congress of IFAC, Beijing, China, Kidlington, UK: Elsevier Sci., Vol. 5, pp. 527-532, 1999

S. Bharadwaj and K. D. Mease, "A New Invariance Property of Lyapunov Characteristic Directions,"Proceedings of the American Control Conference, Vol. 6, pp. 3800-3804, San Diego, June 1999

A. V. Rao and K. D. Mease, "Dichotomic Basis Approach to Solving Hyper-Sensitive Optimal Control Problems," Automatica, Vol. 35, No. 4, pp. 633-642, 1999

S. Bharadwaj, "Geometric Structure of Multiple Time Scale Nonlinear Dynamical system," Ph.D. Dissertation, University of California, Irvine, Aug. 1999

S. Bharadwaj, M. Wu, and K. D. Mease, "Identifying Time-Scale Structure for Simplified Guidance Law Development," AIAA Guidance, Navigation and Control Conference, New Orleans, Aug. 1997

A. V. Rao, "Extension of the Computational Singular Perturbation Method to Optimal Control," Ph.D. Dissertation, Princeton University, June 1996

K. D. Mease, "Geometry of Computational Singular Perturbations", IFAC Symposium on Nonlinear Control Design, Tahoe, June 1995

A. V. Rao and K. D. Mease, "A New Method for Solving Optimal Control Problems", Paper 95-3262, AIAA Guidance, Navigation and Control Conf. , Baltimore, Aug. 1995

A. V. Rao and K. D. Mease, "Minimum Time to Climb Trajectories Using a Modified Sweep Method", Paper 95-3263, AIAA Guidance, Navigation, and Control Conf., Baltimore, Aug. 1995

K. D. Mease, "An Approach to Solving Two Time-Scale Trajectory Optimization Problems", IFAC Workshop on Control Applications of Optimization, Haifa, Israel, Dec. 1995

K. D. Mease, "An Approach to Solving Two Time-Scale Trajectory Optimization Problems," IFAC Workshop on Control Applications of Optimization, Haifa, Israel, Dec. 1995

A. V. Rao and K. D. Mease, "Minimum Time to Climb Trajectories Using a Modified Sweep Method," Paper 95-3263, AIAA Guidance, Navigation, and Control Conf., Baltimore, Aug. 1995

A. V. Rao and K. D. Mease, "A New Method for Solving Optimal Control Problems," Paper 95-3262, AIAA Guidance, Navigation and Control Conf. , Baltimore, Aug. 1995

K. D. Mease, "Geometry of Computational Singular Perturbations," IFAC Symposium on Nonlinear Control Design, Tahoe, June 1995

 


Flight Dynamics and Control Lab Flight Dynamics and Control Lab

 University Of California, Irvine

To contact Professor Mease: kmease@uci.edu